3. Dynamic decoding

3.1 Introduction

The processing step after the acoustic classification is the dynamic decoding. These are the methods which are used to incorporate the dynamic constraints imposed by the HMM part of the hybrid HMM/ANN. Paper 3 covers in detail the dynamic decoding methods used in the WAXHOLM system and several of the included papers (see also section 6.1). The most basic and wide-spread method is the Viterbi algorithm. It finds the most likely path of HMM-states for an utterance. A more accurate method is to compute the most likely sequence of phones or words given the utterance, summed over all state sequences. However, this method is too computationally demanding for all but the simplest applications. The Viterbi algorithm is discussed in the next section, 3.2. Section 3.3 deals with the method used in several of the included papers for finding multiple promising hypotheses instead of only the most likely one (the A* algorithm). Multiple hypotheses constitutes a better interface for information exchange between the recognizer and higher levels of the application. This is because the top-down constraints accessible in the higher levels can then be utilized (e.g., Hetherington, Phillips, Glass and Zue, 1993; Murveit, Butzberger, Digalakis and Weintraub, 1993; Ney and Aubert, 1994). In section 3.4, an efficient storage format for the multiple hypotheses is discussed, and in section 4 the methods presented in (Ström, 1995) for minimization of the storage are covered.

3.2 Viterbi decoding

The Viterbi algorithm (Viterbi, 1967) solves the problem of finding the most likely sequence of HMM-states given a sequence of acoustic input observations, i.e., an utterance to recognize. It is the standard decoding scheme used in different flavors in virtually all state-of-the-art recognition systems. To understand the Viterbi algorithm it is useful to think of the decoding problem as an optimal path-search in two dimensions – time-points and HMM-states. 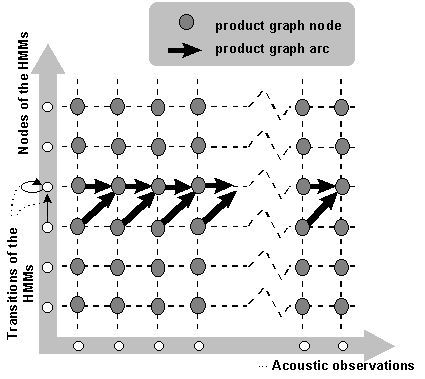Figure 5 shows the states of the HMMs of a recognizer duplicated for each time-point, and lined up in columns. This graphical construct was introduced in (Ström, 1994a) and was named the "product graph" because the nodes are the Cartesian product of the nodes of the HMMs and the time-points. In Paper 3, I account in detail for how the best path is found in the 2-dimensional grid of Figure 5. The general principle is dynamic programming (DP), which yields a time-synchronous search, i.e., time-points are processed one at a time. Therefore the search can be performed in real time as the speaker utters a sentence. This is an important feature in human/machine dialogue where short response times often are critical for users’ acceptance of the systems. The Viterbi search is the most computationally demanding part of the dynamic decoding of the system described in Paper 3, but several approximations are used to keep computation down. The most important one is beam pruning. A combination of two different pruning criteria – both a threshold on the path probabilities and a maximum number of alive paths – are enforced. A section of Paper 3 is devoted to this topic that is of great importance for fast computation. It is shown that the combination of the pruning criteria is more efficient than each criterion by itself.			Figure 5. The product graph. This graphical construction visualizes the Viterbi search. The nodes of the product graph are the Cartesian product of the HMM-states and the sequence of acoustic observations. The Viterbi search is a DP search to find the most likely path through the graph. In the figure, only two of the many transition arcs of the HMMs are shown. The corresponding arcs of the product graph are also drawn. Details of the construction of the product graph is found in Paper 1 and Paper 3.

3.3 The N-best paradigm and A* search

A human/machine dialogue system is a large and complex software program that is impossible to construct and maintain without a great deal of modularity. For example, the ASR module takes audio speech input and delivers a symbolic representation of the utterance as its output. Interpretation of the meaning of the utterance is left to higher level modules. The symbolic representation can simply consist of the most likely string of words computed by the Viterbi algorithm. However, because the ASR module does not necessarily have access to information about the current dialogue state, or a deep syntactic, semantic and pragmatic analysis of the utterance, this is probably not the optimal interface to other modules. An output representation that takes better advantage of the acoustic evidence is one where the ASR module delivers a set of acoustically scored hypotheses to higher modules. These modules can then select the most likely word-string hypothesis on the basis of both the acoustical evidence computed by the ASR module, and the syntactic, semantic and pragmatic analysis. A popular representation of this set of hypotheses is an N-best list. This is simply a list of the N most likely word strings given the sequence of acoustic observation vectors. Thus, an N-best list is a generalization of the output of the Viterbi algorithm (in the case of the Viterbi algorithm, N = 1). Finding the N-best word-strings is a significantly harder problem than just finding the most likely word-string. It can be solved by extending the DP search and keeping a stack of hypotheses at each search point in Figure 5 instead of just the most likely as in the standard Viterbi algorithm. This has the advantage of preserving the time-synchronous feature of the Viterbi algorithm, but the complexity is proportional to N, i.e., the already computationally demanding algorithm becomes slower in proportion to the desired number of hypotheses. A more computationally efficient method is the so called A* (a-star) search. This method is based on the stack decoding paradigm where a search tree is built with partial hypotheses represented by paths from the root to the leaves. The word-symbols are associated with the branches of the tree (see Figure 6). During the search, most paths are partial hypotheses, i.e., they do not cover the whole utterance. The partial path that is most promising according to a search heuristic is expanded by growing new branches from its leave. When there are enough complete paths in the tree, the search is terminated. The key to an efficient A* search is the search heuristic. When evaluating partial paths, the likelihood of the words in the path so far, given the acoustic observation, is easily accessible and should of course be utilized. But it turns out that this is not enough - it is also necessary to estimate the influence of the remainder of the utterance. It is possible that a partial path with a high likelihood turns out to be in a "dead-end", and can not be completed with a high likelihood. It was an observation of Soong and Huang (1991) that made A* practically applicable to the N-best problem in ASR. They realized that the likelihoods computed in the Viterbi algorithm constitute a particularly well behaved A* heuristic. In the Viterbi search, the highest likelihoods of the observations from the beginning of the utterance to all points in the product graph (see Figure 5) are computed. If the A* search is performed backwards from the end of the utterance, the partial paths are from some interior point to the end of the utterance, and the remainder of the utterance is from the beginning to the interior point. Thus, the best possible likelihood for the remainder of the utterance is the likelihood computed in the Viterbi search. This particular heuristic has many attractive features, one is that complete paths are expanded in order of likelihood, i.e., when N complete paths with different word strings have been expanded, the search can be terminated. The development of an A* search algorithm, currently used in the WAXHOLM dialogue system has been a significant part of my work in the ASR field, and is reported on in Paper 1 and Paper 3. The most original aspect of the work in this area is the optimization of the "lexical network", introduced in Paper 1, that greatly reduces computation in the search. The optimization method is developed further in Paper 3, where the concept of word pivot arcs is introduced. Although in this case it is used only in the A* framework, word pivot arcs are relevant also in standard Viterbi decoding, because they can be used to significantly reduce the size of the product graph.
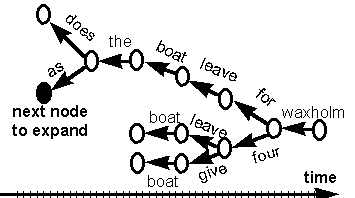
			Figure 6. The search tree of a stack-search backwards from the end of an utterance. During the search, the tree is expanded by selecting the most "promising" leave and grow new word-branches from it. The key to a successful algorithm is how to determine which leave is the most promising. See the main text for details.

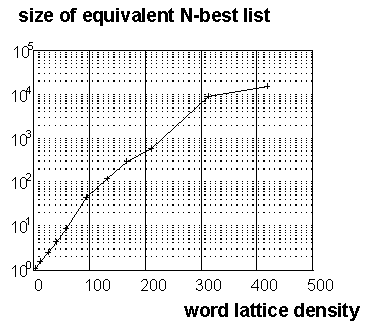
3.4 Word lattice representation of multiple hypotheses Passing N-best lists from the ASR module as the recognition result to higher level modules is a step that increases the coupling between the modules without decreasing the modularity. It is a clean interface between modules, but in some cases the entry in the N-best list that is optimal after considering knowledge sources provided by higher level modules, is very far down the list. Thus, it is necessary to pass long lists between the modules. 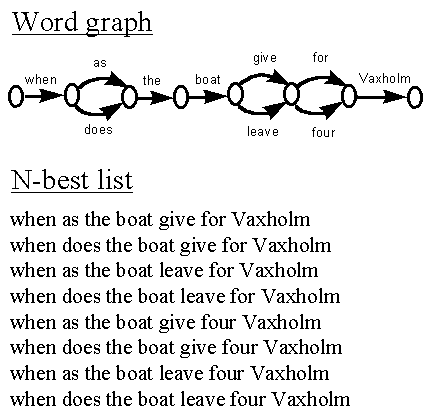In this case, a so called word-lattice or word-graph is a better representation of the hypotheses because it is more compact (see Figure 7 and Figure 8). In Paper 3, the A* search is modified to produce a word-lattice instead of an N-best list. A word lattice is a graph that generates all hypotheses, including all time-alignments of the words, above a likelihood threshold. This is the method now used in the WAXHOLM demonstration system (see section 6.1). The dialogue module of the WAXHOLM system requires an N-best list as input, but this is computed in a subsequent search in the word-lattice. The direct construction of a word-lattice in the A* search gives a cleaner implementation, but also improves the performance. It is computationally advantageous to make a separate search for the N-best hypotheses in the produced word-lattice instead of producing the list while performing the first A* search. The reason is that finding the N-best list is inherently an exponential complexity problem while constructing the word-lattice is of polynomial complexity (this is discussed in Paper 3).			Figure 7. Two different representations of a set of hypotheses. From this simple example, the difference between the two formats is clearly seen. The entries in the N-best list are typically similar to each other, therefore it is sometimes practical to work with the more compact word graph representation.
			Figure 8. This graph shows the size of the word lattice (number of arcs per word) versus the number of entries in an hypothetical N-best list covering the same hypotheses. It is easy to see the benefit of the word lattice for large sets of hypotheses. The example is taken from Paper 3.