4. Word graph minimization

This section is an extended version of the summary (Ström, 1995) of a presentation at the IEEE Workshop on Automatic Speech Recognition, 1995. This extended material has not been published before.

4.1 Introduction

With the development of complex speech technology applications, the ability of an automatic speech recognition (ASR) system to output multiple recognition hypotheses is becoming increasingly important. Examples of such applications are human/dialogue applications and machine translation where the ASR must interact with modules that handle discourse, semantics and pragmatics. Passing multiple recognition hypotheses to the higher levels of the system is a way of increasing the coupling without decreasing the modularity, which is essential for the development of large complex systems.

Another use is hypothesis re-scoring, where the multiple hypotheses are an internal, intermediate representation generated by a fast initial search. These are then used to limit the search-space in a second, more accurate search.

Word-lattices and word-graphs provide a compact representation of sets of hypotheses as described in section 3.4. I will mean by a word-lattice, a word graph that contains all time alignments that have a likelihood above the pruning threshold.

For re-scoring using new acoustic models, the word-lattice constructed in the A* search is a good representation because in this case, it is necessary to re-score the different alignments. However, if the objective is re-scoring using only a new grammar, the multiple time-alignments are excessive, and a more compact representation is better.

4.2 Problem formulation

It is not trivial to define a measure of size for word-graphs. From a practical point of view, the size of the graph should reflect the amount of computation required to perform critical operations on the graph. Such an operation may for example be searching for the most likely path through the graph. The number of arcs is in many cases a good indication on the amount of computation required, and a wide-spread measure of word-graph size is lattice density. The lattice density of a word-graph is the number of arcs divided by the number of words actually uttered (Ney and Aubert, 1994).

Another measure of size is the number of nodes in the graph. In contrast to the number of arcs, the number of nodes has typically only a small impact on the computation required for search operations. Instead the memory requirement of the algorithms is affected because search algorithms often store state-information for the nodes at each time-frame.

If the objective is re-scoring word-graphs with a new grammar, the time-alignments of words is not important and it is therefore desirable to reduce the size as much as possible without altering the generated set of word-strings. Thus, the problem can be defined as finding the word-graph with the minimum number of arcs or nodes that generates exactly the same word-strings as a given word-lattice.

4.3 Approximative methods

A word lattice is a directed acyclic graph (DAG) - a subclass of non-deterministic finite state automatons (NFA) (see for example Hopcroft and Ullman, 1979). Minimizing an NFA is a hard problem that can not in general be solved in polynomial time. Therefore, the problem has been attacked using heuristic methods that reduce the graph but not to its minimal size.

In the word-pair approximation (Ney and Aubert, 1994), it is assumed that the positions of word boundaries are independent. In most cases this is a sound assumption, but it may lead to search errors for short words and when a minimum duration constraint is enforced for phones.

In the A* search by Hetherington, Phillips, Glass and Zue (1993), arcs are not added to a node of the word-graph if they do not introduce a new partial word-sequence. This reduces the constructed graph significantly.

4.4 The minimal deterministic graph

Although the approximate methods can be quite effective, it is not satisfactory to settle with an approximation without having established a baseline with an exact method. A well-known minimization algorithm exists for minimizing NFAs. The procedure results in a minimal (with respect to the number of nodes) equivalent deterministic finite automaton (DFA). This is a well defined objective, and in addition the deterministic property of the resulting graphs has some other nice effects. The algorithm (Hopcroft and Ullman, 1979) can be broken down into two steps. The first step is to construct an equivalent deterministic finite state automaton (DFA) - the "determinization". A deterministic FSA has the property that, given a sequence of words, there is at most one path through the graph that generates it. This is accomplished for example by allowing only one start state and no more than one out-flowing arc for each word from any state. The second step is minimization of the DFA to obtain the minimal deterministic graph - the minimization. The resulting reduction of the number of connections in the graph can be seen in Figure 9. In this example the reduction is about 50 times, but this is likely to be a problem dependent number. Of the two steps, the determinization is the computationally hardest. In general the determinization can not be done in polynomial time or space. But as we will see, the particular structure of word-graphs can be utilized to attain an acceptable computational cost. The minimization algorithm has N log(N) complexity in general, but in the case of word-graphs this can be reduced to approximately linear complexity. In the next two sections the two steps are reviewed briefly. A more thorough account of the classic algorithm can be found in (Hopcroft and Ullman, 1979). Here we focus on the aspects that are specific to optimizing word-graphs - the short-cuts due to the special structure of word-graphs, and computational considerations given this particular type of NFA.			Figure 9. Size of the minimal deterministic graph as a function of the size of the original lattice. Sizes are measured in arcs per word - lattice density. This example was produced by running the ASR of the WAXHOLM dialogue system with varying pruning threshold. This figure is taken from Paper 3.

4.5 Determinization

The key to the determinization algorithm is the identification of sets of nodes on the original graph with single nodes in the resulting deterministic graph. This is also what causes the exponential computational complexity as there are 2^N sets of nodes in an original graph of N nodes. Luckily, all sets will not be considered during the construction of the deterministic graph. Still, the main effort in the implementation of the algorithm involves the storage of sets of nodes in an efficient manner.

To simplify the algorithm slightly, we assume that there is exactly one start node and one end node in the graph. This can easily be enforced in the case of word-lattices, in particular if all utterances must begin and end with the special "silence" symbol.

The algorithm can now be described as follows:
Identify nodes n_iof the deterministic graph with sets of nodes N_i in the original latice.
Define N₀ to be the set containing only the start node of the lattice, and N_endto be the set containing only the end node of the lattice.
Initialize the deterministic graph with the node n₀.
For each node, n_x in the deterministic graph and each word w

N_y

N_x

n_x

n_y

The procedure is illustrated in Figure 10.

Computationally, the greatest problem is how to store the sets of nodes in an efficient manner. It is important to be able to quickly determine if a set already exists, or if it represents a new node in the deterministic graph. In the implementation, this was solved by a combination of a hash-table and comparing sorted sets of nodes. The hash table is based on a hash-key that is independent of the order of the nodes, and the sets are not sorted unless necessary. This means that whenever an already existing set is looked up, it will be necessary to sort it and the lists with the same hash-key among the already existing. But no sorting is needed to insert a new set unless a hash-table clash occurs. Because large sets are likely to be looked up only once, the effect is that larger sets are seldom sorted.

4.6 Minimization

The deterministic graph constructed in the previous section can now be minimized by considering the partial word sequences that can be generated forward from each node. We define for any path of arcs from a particular node to the end-node, the sequence of words on the arcs as generated by the node forward.

Any pair of nodes that generates exactly the same word-sequences can clearly be merged without changing the set of complete word-sequences generated by the graph. The special structure of word-graphs makes this merging particularly simple. Because all arcs flow from left to right, the nodes are processed from right to left. It is then guaranteed that when processing a particular node, all nodes to the right of it that can be merged, are in fact already merged. Therefore, all nodes to the right of the current node generate different sets of sequences forward.

The notion of "left" and "right" can be formalized by introducing maximum and minimum depth. This is the length of the shortest and the longest word sequence generated from the node (see Figure 11). Only nodes that have exactly the same maximum and minimum depth need to be considered for merging. Further, if nodes are processed in order of increasing minimum depth, all that needs to be compared is the words on the out-flowing arcs and the node that they flow to. There is no need to consider more than one arc forward because all nodes forward generate different word-sequences. The procedure of merging nodes is illustrated in Figure 12 where the deterministic graph constructed in Figure 10 is continued with the minimization step.

In general, the minimization step has N log(N) computational complexity. However, because of the directed acyclic structure of word-graphs and the distribution of word duration, the number of nodes with identical maximum and minimum depth is approximately a linear function of utterance length.

4.7 Computational considerations

As noted earlier, the determinization procedure has, in the worst case, exponential computational complexity with respect to the number of nodes. However, the input lattice-size has at least two distinguishable dimensions: the utterance-length and the graph-density (number of arcs per utterance-length) (Ney and Aubert, 1994). Graph-density corresponds to the amount of pruning and utterance-length corresponds to the length of the input. Of the two, the length of the input is varying, but the amount of pruning can be controlled in the A* search.

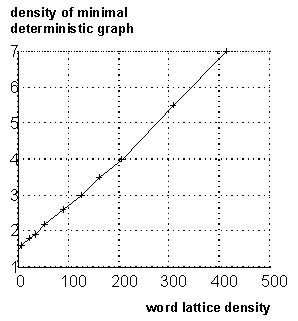
We studied empirically the time-complexity of the construction of the DFA in the 1000-word spontaneous speech task of the WAXHOLM-project (Blomberg et al., 1993; Paper 3). In the top graph of Figure 13 the exponential behavior can be seen, but the bottom graph shows approximately linear time-dependence with respect to utterance-length when the dependency of the graph-density have been eliminated. This difference in behavior for the two dimensions is very important because it gives us the possibility to control the "exponential explosion" of the algorithm by tuning the pruning.

For comparison, the word-pair approximation was also investigated. Applying the word-pair approximation to the word-lattice resulted on average in a reduction in the number of arcs to 8.1% of the original lattice. The minimal deterministic graph for the same word-lattice was on average reduced to 1.4% of the lattice.

4.8 Discussion

The exact minimization algorithm investigated in this study was clearly shown to produce smaller graphs than the approximate word-pair approximation method. This is true in spite of the fact that the exact algorithm minimizes the number of nodes, but the two methods are compared on the basis of the number of arcs. In the example investigated, the exact algorithm produced almost six times smaller graphs than the approximate method, but the exact quotient is likely to be dependent on the lexicon, pruning aggressiveness etc.

In contrast to the word-pair approximation, the graph of the proposed algorithm generates exactly the same word-strings as the original lattice (no hypotheses are lost by approximation). However, since the proposed method is exponential with respect to lattice-density, a hybrid-approach where the lattice is first reduced by the word-pair approximation and then minimized, seems to be an attractive alternative.

The computational demands of the exact minimization are probably too high for use in the on-line recognition mode of a real-time ASR system (with contemporary computer technology). However, for off-line tasks, where the same minimized word-graphs are used repeatedly, the effort may be worthwhile. Iterative estimation of grammar parameters during training of the system is one example.

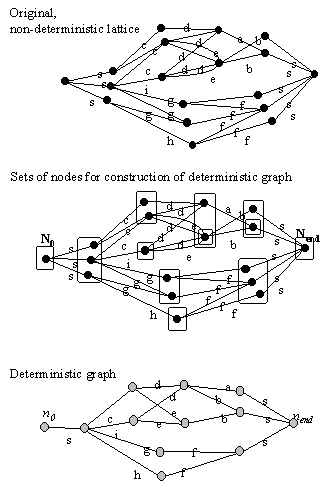Figure 10. Illustration of the determinization algorithm. The set N₀ is the first to be taken care of in step 4, and there is only words labeled "s" flowing out from it so w=s. The set of nodes reached by the s-arcs is the next node of the deterministic graph. This set in turn has four different words flowing out from it (c, i, g, h), and four corresonding new sets are formed. The process continues until no new sets are formed.

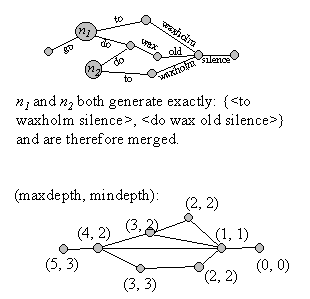
Figure 11. Illustration of the minimization. For each pair of nodes it is checked if they generate exactly the same set of partial word-sequences forward. Because word-graphs are acyclic, it is possible to efficiently compute the longest and shortest generated word-sequences generated forward from each node (max and min depth). This reduces the number of node-pairs to compare significantly because only those with the same maximum and minimum depth need to be considered.

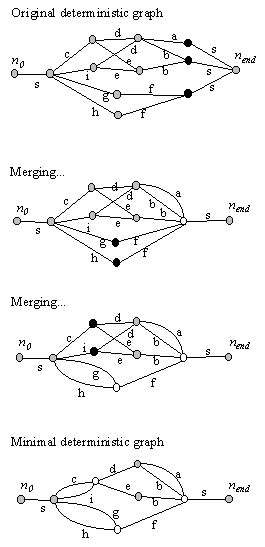Figure 12. Illustration of the merging of nodes in the minimization step of the algorithm. Merging proceeds from right to left and because all nodes to the right are merged if possible, it is easy to check if two nodes generate the same word sequences forward. See the main text for details.

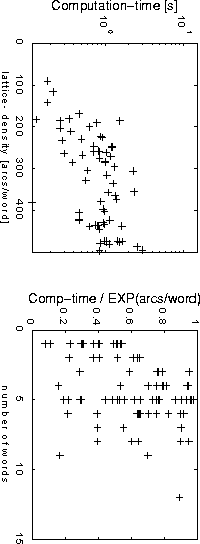
Figure 13. Top: Time for construction of the DFA as a function of the lattice-density. Bottom: Construction time divided by the exponential of the lattice density. The simulation was made on a SPARC 10 workstation. This figure is taken from Ström (1995).