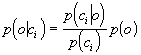 |
(1)
|
| nikkostrom | NICO | Quite BASIC |
| This paper presents new methods for training large neural networks for phoneme probability estimation. A combination of the time-delay architecture and the recurrent network architecture is used to capture the important dynamic information of the speech signal. Motivated by the fact that the number of connections in fully connected recurrent networks grows super-linear with the number of hidden units, schemes for sparse connection and connection pruning are explored. It is found that sparsely connected networks outperform their fully connected counterparts with an equal or smaller number of connections. The networks are evaluated in a hybrid HMM/ANN system for phoneme recognition on the TIMIT database. The achieved phoneme error-rate, 28.3%, for the standard 39 phoneme set on the core test-set of the TIMIT database is not far from the lowest reported. All training and simulation software used is made freely available by the author, making reproduction of the results feasible. |
Recurrent connections are not the only path to good results, but other existing solutions have different problems. Another architecture is used with good results in [2]. There, time-delay windows [4] are used instead to capture the temporal cues of the speech signal. The absence of recurrent connections makes the training algorithm more stable, but very large networks are used to achieve good results, and therefore the available computing resources limits the performance.
In contrast to the existing high performing ANN solutions, the well-established Maximum Likelihood (ML) training paradigm for the standard HMM (e.g. [5]) has a robust, theoretically well established training scheme and must be considered a safer route to a functioning speech recognition system today. The HMM paradigm also has the advantage of a large mature body of easily available software.
The aim of this paper is to describe new methods for robust
training of large, high performance ANNs using limited computing resources,
i.e., reduce the problems of contemporary ANN solutions. Further, the software
tool-kit used for training and evaluating the neural networks is made freely
available to promote further development in the field.
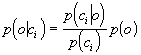 |
(1)
|
Basically, a one-state Markov model is used for each phoneme and the transition probabilities are estimated by ML of the durations of the training database. In addition to this weak duration model, a phoneme-dependent minimum duration constraint is imposed by adding extra nodes to the HMM and putting the self-loop on only the last node. The minimum durations are selected such that 5% of the phones in the training data are shorter than the minimum. This fraction was chosen, after some experimenting, to optimize recognition performance. A phoneme bi-gram grammar is used for the transition probabilities between phonemes.
The a posteriori phoneme probabilities are estimated by the output units of an ANN with 10 ms frame resolution. A feature vector is computed from each frame including the twelve first Mel cepstrum coefficients and the log energy. The input to the ANN is the feature vector and its first and second time derivatives. More details about the signal processing, the estimation of the HMM parameters and the dynamic decoding is given in [6].
Recurrent neural networks (RNN) is a different course to utilizing the context in the classification and are currently the most successful architecture for phoneme recognition [3]. In RNN, units in the same layer are connected to each other with a time-delay of one. This approach differs from TDNN in that the activity of a unit depends recursively on activities at all previous times.
TDNNs and RNNs have much in common; in particular, both use time-delayed connections to incorporate context into the classification. If the connections of an RNN can have multiple time-delays instead of just one time step, the resulting network has all the modeling power of both architectures. This unified architecture, RTDNN, introduced in [7], is used in this study.
In the RTDNN framework we attempt to preserve the best features of the TDNN and RNN structures. The concept of look-ahead connections is borrowed from TDNN. It simplifies ANN design because it makes delayed targets unnecessary and the dynamic structure more intuitive. Look-ahead connections force some unit activities to be computed ahead of others, but the network is still a feed-forward network as long as no unit's activity at a particular time depends on its own activity.
A way to visualize back-propagation through time is to draw the spatial dimension of the network in one dimension, i.e., line up all units in one column. Then unfold the network in the time dimension by drawing one column of units for each time point. Figure 1 shows a very simple example of such an unfolded network. The unfolded network is similar to a network with no delays but as many layers as there are time points. The difference is that the connection weights are shared by all connections that correspond to the same connection in the original network. Back-propagation through time is equivalent to standard back propagation with this additional weight sharing constraint.
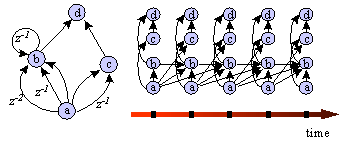
Figure 1. A simple dynamic network (left)
and the same network unfolded in time (right) where the units a-d are duplicated
for each time-point. Connections labeled z-x are delayed x time points.
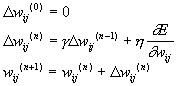 |
(2)
|
The picture becomes more complicated for back-propagation through time because the derivatives depends not only on the current pattern but on the whole sequence of patterns. We have adopted the approximate scheme to update the weights every N frames, i.e., approximate the derivative based on sub-sequences of the training data. This method is also used in [3]. The approximation is worse if the weights are updated frequently, but on the other hand it is desirable to update frequently, to speed up training. In the simulations, the weights are updated every 20-30 frames (N is random distributed R[20;30]). This is intuitively reasonable as it corresponds to the length of a syllable.
To reach a minimum of E, the gain parameter must be gradually decreased during the training. We have combined this with cross-validation in a manner similar to [2]. The idea is to decrease the gain parameter when the objective function fails to decrease on a validation set. To be more specific, the training data is partitioned into a training set and a smaller validation set. The training set is used for the actual back-propagation training, and after each epoch, the error function E is computed for the validation set too (without weight updating). If E fails to decrease during an epoch, the gain parameter g is multiplied by a constant factor a < 1. In this study a is always 0.5, h is 0.7, and the initial value of g is 10-5.
| 39 * H* 7 + H * H * 3 + H * 61 * 3 = 456H + 3H2 |
(3)
|
Connection pruning is a method that reduces the runtime of trained networks. The most well-known method is optimal brain damage (OBD) [9]. An overview of this and other methods is found in [8]. In our experiments a coarse pruning criterion is used - we simply remove all weights smaller (in magnitude) than a threshold. It is important that the network is retrained after pruning. This training converges much faster than the original training, and the retraining corrects most of the errors due to the simplistic pruning criterion.
Unfortunately, pruning has no impact on training time because it is applied after training. To reduce training time we have experimented with sparsely connected networks. Before training, there is no available information about which connections are salient, so a random set of connections must be selected. Of course, this is in general not the optimal set, but as will be seen in section 5, the resulting ANN may still be competitive.
A straight-forward, random connection scheme is to consider all connections in a hypothetical, fully connected network and let each be a connection in the actual sparse network with probability f (connectivity). The expected number of connections in the sparse network is then Nf, where N is the number of connections in the fully connected network. In [10] it is pointed out that the sparse connectivity has the effect of decoupling the output units, i.e., all output units are not connected to the same hidden units. Results from several comparative studies are reported, and sparsely connected networks perform as well as, or better than both OBD and fully connected networks.
In RNNs, the number of connections is proportional to the square of the size of the hidden layer (the second term of (3)). Thus, for large hidden layers, a very low connectivity is necessary to reduce connections to a manageable number. This reduces the network's functional capacity more than can be compensated for by the increased number of hidden units.
To overcome the square relationship between the layer
size and the number of hidden units, we introduce localized connectivity.
In this scheme, recurrent connections between unit u1
and u2 are added with the probability
|
(4)
|
The results are shown in Figure 2. The underlined error-rates clearly show how the fully connected network is outperformed by sparsely connected ANNs with an equal number of connections. A set of networks with 300 hidden units are evaluated to compare different sparse connection schemes. The sweep over varying hidden layer size from 100 to 600 units, with accompanying decrease in error-rate, show the benefit of being able to work with large hidden layers. Because of limited computing resources, we have not yet trained ANNs with more than 600 units, but because the error-rate is constantly decreasing, we expect larger networks to perform even better. The lowest rate, 28.3%, is already better than all reported HMM-based results, e.g., [11] (30.9%), but not quite as low as the currently lowest reported RNN result [3] (26.1%).
The two rightmost columns of Figure 2 are designed to test the idea of [10] that connection to higher layers should be more sparse than lower layers, in order to decouple the output units. Their hypothesis is supported by our experiment and will be put to use in future studies.
In a separate experiment, connection pruning was applied to the networks, and it was found that with a weight threshold of 0.08, the number of connections is reduced by circa 50% for all networks. After retraining, the error-rate had never increased by more than 1%.
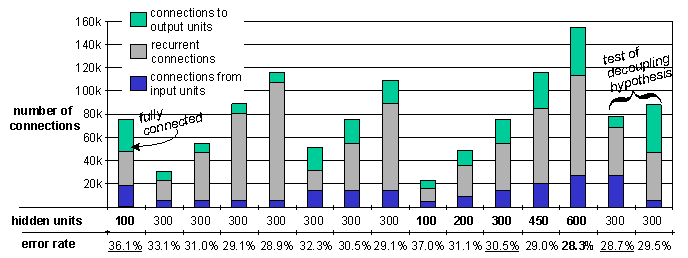
Figure 2. Phoneme
recognition results for the core test set of the TIMIT database. The 39
symbol set, also used in [3] and [11] is used. Error-rate is defined as
the sum of insertions, deletions and substitutions per phone.
[2] Bourlard H. & Morgan N., "Continuous Speech Recognition by Connectionist Statistical Methods", IEEE trans. on Neural Networks, 4(6), pp. 893-909, 1993.
[3] Robinson A.J., "An application of Recurrent Nets to Phone Probability Estimation", IEEE trans. on Neural Networks, 5(2), pp. 298-305, 1994.
[4] Waibel A., Hanazawa T., Hinton G., Shikano K. & Lang K., "Phoneme Recognition Using Time-Delay Neural Networks," ATR Technical Report TR-006, ATR, Japan, 1987.
[5] Young S., Jansen J., Odell J., Ollason D. & Woodland P., "HTK - Hidden Markov Toolkit", Entropic Cambridge Research Laboratory, 1995.
[6] Ström "Continuous speech recognition in the WAXHOLM dialogue system", STL-QPSR 4/1996, pp. 67-95, KTH, Dept. of Speech, Music and Hearing, Stockholm, Sweden, 1996.
[7] Ström N., "Development of a Recurrent Time-Delay Neural Net Speech Recognition System", STL-QPSR 2-3/1992, pp. 1-44, KTH, Dept. of Speech, Music and Hearing, Stockholm, Sweden, 1992.
[8] Thimm G. & Fiesler E., "Evaluating pruning methods" , In 1995 International Symposium on Artificial Neural Networks, Proc. ISANN '95, pp. A2 20-25, National Chiao-Tung University, Hsinchu, Taiwan, 1995.
[9] Le Cun Y., Denker J. S. & Solla S. A., "Optimal brain damage", In Advances in Neural Information Processing Systems, II, ed: Touretsky D. S., pp. 589-605, San Mateo, California IEEE, Morgan Kaufmann, 1990.
[10] Ghosh G. & Tumer K., "Structural adaptation and generalization in supervised feed-forward networks", Journal of Artificial Neural Networks, 1(4), pp. 430-458, 1994.
[11] Lamel L. & Gauvain J. L., "High performance speaker-independent phone recognition using CDHMM", Proc. EUROSPEECH, pp. 121- 124, 1993.