| nikkostrom | NICO | Quite BASIC |
Nikko Ström (1997): "A Tonotopic Artificial Neural Network Architechture for Phoneme Probability Estimation," Proc. of the 1997 IEEE Workshop on Speech Recognition and Understanding, pp. 156-163, Santa Barbara, CA.
Nikko Ström
Department of Speech, Music and Hearing,
Centre for Speech Technology,
KTH (Royal Institute of Technology),
Stockholm, Sweden
| Abstract - A novel sparse ANN connection scheme is proposed. It is inspired by the so called tonotopic organization of the auditory nerve, and allows a more detailed representation of the speech spectrum to be input to an ANN than is commonly used. A consequence of the new connection scheme is that more resources are allocated to analysis within narrow frequency sub-bands - a concept that has recently been investigated by others with so called sub-band ASR. ANNs with the proposed architecture have been evaluated on the TIMIT database for phoneme recognition, and are found to give better phoneme recognition performance than ANNs based on standard mel frequency cepstrum input. The lowest achieved phone error-rate, 26.7%, is very close to the lowest published result for the core test set of the TIMIT database. |
The choice to represent the input speech spectrum by a small set of features is an inheritance from the standard Continuous Density HMM (CDHMM). In a CDHMM, a small number of approximately orthogonal features make a good input representation because of the properties of the model and the statistical training methods. The same type of arguments can be used for choosing a smoothed input representation also in the case of a hybrid HMM/ANN system - an ANN with a too detailed input representation runs a higher risk of learning details of the speech in the training corpus that do not generalize to speech from new users of the trained system. However, as the results of this paper indicate, this is not necessarily true for ANNs that are not fully connected.
Although ANNs (multi-layer perceptrons) are general pattern matching devices, the choice of input representation as well as the structure of the ANN, e.g., the number of hidden units and the connectivity between layers, represents a priori knowledge in the ANN, because it puts constraints on the relations that the ANN can learn. Recently, it has been shown that sparsely connected ANN architectures can be used to promote the training of networks with a large number of hidden units. The results of [2,3] indicate that increasing the number of hidden units is more important for the network's performance than to fully connect between the layers. In this paper we turn to the input units. With a sparse connection scheme between the input units and the hidden units, the generalization of the network can be controlled by the connectivity rather than by smoothing the input representation.
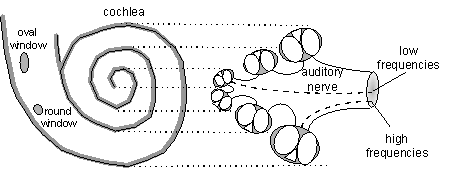
Although ANNs are very different from biological neural systems, human
perception can be an important source of inspiration for innovations in
ANN technology. It has been found that in the auditory nerve, neurones
are organized in an orderly manner depending on their characteristic frequency
[4]. Neurones responding to high frequencies are located in the periphery
of the nerve, and those responding to low frequencies are found in the
center (see Figure 1). This structure of the auditory nerve is called tonotopic
organization. The sparse connection scheme that is introduced in this paper
is based on a similar tonotopic organization of the hidden units of the
ANN.

Figure 1. Tonotopic organization of the auditory nerve. Left: schematic picture of the cochlea. Right: transverse section of the cochlea. Because lower frequencies are closer to the center, the tonotopic organization of the auditory nerve is achieved already in the connection with the cochlea. The center of the nerve is connected to the center of the cochlea (that reacts to low frequencies), and the periphery of the nerve is connected to the outermost loop of the cochlea (that reacts to high frequencies).
In a more complex connection scheme, the connectivity is a function of the two units to connect. An important special case is when a metric is defined on the units, and the connectivity is a function of the distance between the two units. This is called a local connection scheme. In [2,3], a metric was defined on the hidden layer for the connectivity of the recurrent connections. Highest connectivity was assigned for self-connection, and gradually lower connectivity was used for connections between units located at greater distances from each other within the layer. This metric is arbitrary in the sense that it does not reflect some known property of the signal. Still, it was shown to improve the ANN performance significantly.
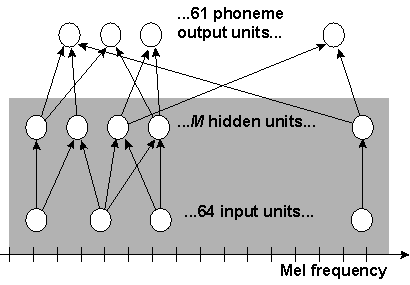
In this study we use a tonotopic metric for both the input and the hidden units. The structure of the ANN is outlined in Figure 2. The input units take the values of the 64 activities of a mel frequency filter-bank. Thus, a significantly more detailed input representation of the speech spectrum is used than what is common for contemporary ASR. The input units are ordered by center frequency, and the metric is simply defined by the position in the 1-dimensional input layer. The hidden layer of units is also 1-dimensional, and a metric on the M hidden units is defined by multiplying the unit's ordering number by 64/M. For example, hidden unit number 17 is located at 17 * 64/M in this metric. Thus, the metric of the hidden units is normalized such that the positions of hidden units are in the same range as input units. Like in the auditory nerve, a characteristic (mel) frequency can now be associated with each hidden unit. We define a tonotopic connection scheme by letting the connectivity for connections between the input layer and the hidden layer be a decreasing function of the distance between the units.
In the experiments, an exponentially decaying connectivity function
is used. The connectivity between input unit number n, in,
and hidden unit number m, hm, is given by:
|
(1)
|
![]()
is the distance between the units, and ![]() input
is a parameter controlling the overall connectivity.
input
is a parameter controlling the overall connectivity.
Except for the tonotopic connection scheme between input units and hidden
units, the ANN architecture is the same as in [2,3]. The temporal features
of the speech are modeled by time-delayed connections. This is described
in detail in [3] and can only be briefly summarized here. Higher layers
have access to the activities within a time-delay window of units in lower
layers. The time-delay window for connections from the input layer to the
hidden layer is seven frames wide, and the window for connections from
the hidden units to the output layer is three frames wide. In addition,
recurrent connections between units in the hidden layer are used with time-delays
one, two and three. The recurrent connections have the same connectivity
function as the connections from the input units, but with a different ![]() ,
i.e.,
,
i.e.,
|
(2)
|
Three ANNs with tonotopic connection, and different hidden layer sizes
were trained and evaluated. Only the number of hidden units was varied,
and the fixed connectivity parameters were: ![]() input
= 15,
input
= 15, ![]() recurrent
= 25, and
recurrent
= 25, and ![]() output
= 0.10.
output
= 0.10.
After training, the networks were pruned in an iterative procedure. It was shown in [2,3] that this not only reduces the computational effort for running the trained networks, but also in some cases improves performance. In each iteration, the network is first pruned by simply removing all connections whose weights fall below a pruning threshold, and then the pruned network is retrained. The pruning threshold is initially small and gradually increased in subsequent iterations. Figure 3 shows the performance versus the network size for the networks with varying number of hidden units and varying amount pruning.
The increase in performance for the moderately pruned networks over the unpruned, that can be seen in some cases in Figure 3, could be due to an improved generalization ability when the number of free parameters are decreased. However, comparison in Figure 3 of the performance on the training versus the test data does not support this; performance improves for both sets in the first pruning iteration. A more likely explanation is that the distortion due to the deletion of connections, help the networks to escape from local optima of the search space. This phenomenon was also seen for some networks in [2,3], and is an unanticipated positive side-effect of the pruning.
The overall results for the four different network sizes are reported
in Table 1. The error-rates for the new, tonotopic ANNs are consistently
lower than for the mel cepstrum based ANNs of [2,3] with the same number
of hidden units, and the tonotopic ANN with the lowest error-rate, 26.7%,
outperforms all cepstrum based networks of [2,3]. Thus, the phoneme recognition
results on the TIMIT database indicate that the new approach is superior
to the standard mel cepstrum architecture that was used in our earlier
studies. The lowest phone error-rate of this study, 26.7%, is very close
to the (to our knowledge) lowest published rate, 26.1%, reached
by another ANN based system [8]. Results reported for other methods are
slightly higher, e.g., 26.6% [7] using a segment based approach and 27.7%
[8] with a CDHHM recognizer (the latter was achieved for the full test
set - a slightly easier task).
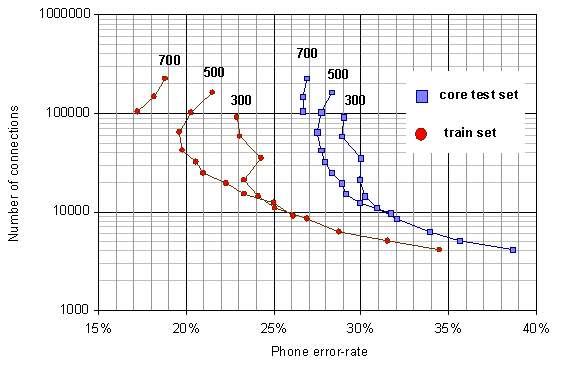
Figure 3. Phone error-rate versus number of connections. The number
above each data series indicates the number of hidden units. Connected
points indicate different amount of pruning of the same original network.
Note that the optimal amount of pruning (that gives the lowest error-rates)
does not differ for the training and test set. The optimal network can
therefore be selected during training.
| Number of hidden units |
300
|
500
|
700
|
| Number of connections in the unpruned network |
91,038
|
161,665
|
228,102
|
| Number of connections in the optimal, pruned network |
58,346
|
64,507
|
149,220
|
| Phone error-rate
(TIMIT core test set) |
28.9%
|
27.5%
|
26.7%
|
| Phone error-rate
(full TIMIT test set) |
28.2%
|
26.5%
|
25.9%
|
Table 1. Lowest phone error-rates for the three different sizes of
the ANN with tonotopic connection. The error-rates reported here are for
the optimal amount of pruning for each hidden layer size (see Figure 3).
Recently, a method that processes sub-bands individually, and recombines the recognition based on the sub-bands at a higher level of the recognizer, have been proposed [9,10]. The method has similarities with our approach, but sub-band recognition has not so far been used with the high resolution of the input representation that is utilized in the tonotopic ANN. In [9,10] it is reported that sub-band ASR is most effective for corrupted or noisy speech. This is promising as the TIMIT evaluation of our study is performed on clean speech. In the future we will experiment with tonotopic ANNs also for noisy speech.
The focus in this paper has been on the low error-rates for the optimal, pruned networks with about 50,000 to 100,000 connections. However, the smaller, more aggressively pruned networks can also be useful, e.g., in an initial fast search in a multi-pass recognizer, or in cases when CPU time is limited. Better than 30% phone-error rate can be achieved with less than 15,000 connections.
Keeping in mind that this is the first study of the architecture, the recognition results are very encouraging. Many parameters that can be varied have not been optimized, e.g., the filter shapes and number of filters of the filterbank, the particular shape of the local connectivity distribution, and the relative connectivity for the different types of connections of the ANN. Also the parameters of the annealing scheme in the pruning process are important, because pruning was shown to not only improve computational efficiency, but also accuracy. We expect further studies to better reveal the full potential of the method.